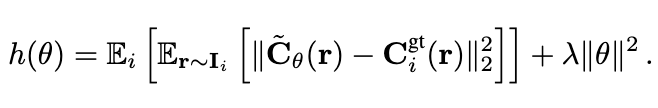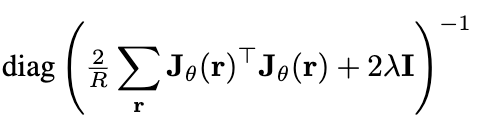To parametrize possible perturbations on a pre-trained NeRF (with optimized parameters φ∗) and then analyze if in fact a part of the reconstructed NeRF can be perturbed, we introduce a spatial deformation layer (parametrized by θ) on the input coordinates of NeRf, formalized as below:
where deformation layer is modeled as a tri-linearly interpolatable grid. We assume a likelihood of the same form as with the NeRF parametrization,
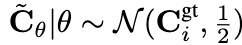
. To ensure small perturbations, we place a regularizing independent Gaussian prior
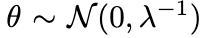
on our new parameters:
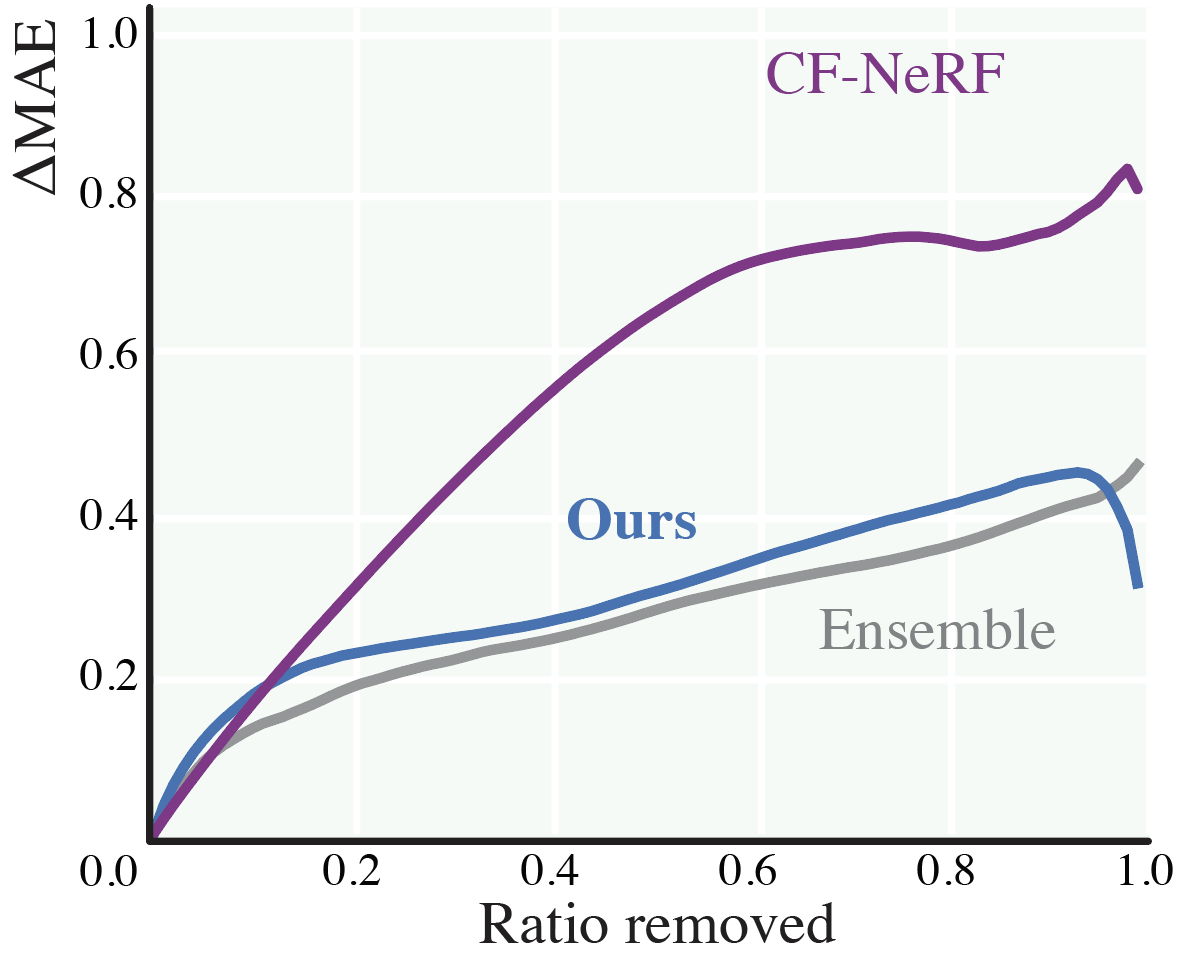
It is now possible to minimize the negative log likelihood term above wrt to θ and with φ∗ frozen, to converge to one of the many valid solutions for the spatial perturbations on a given NeRF that do not affect reconstruction loss. The more freely a perturbation at a point can move the point (i.e bigger variance in the perturbation), the more uncertain we are about the true position of that reconstructed point in the space.
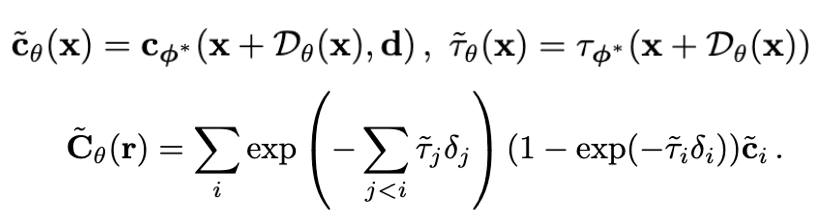
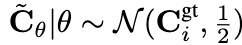 . To ensure small perturbations, we place a regularizing independent Gaussian prior
. To ensure small perturbations, we place a regularizing independent Gaussian prior 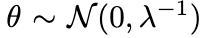 on our new parameters:
on our new parameters: